The Gambler’s Fallacy: How It Affects Lottery Play
As a species, we fail at grasping the meaning of chance.
Sure, we recognize randomness, but we ignore it more often than one cares to admit. We are creatures of logic, after all – in our minds, it follows that “A” must lead to “B,” and so on.
In other words, even in the most random of events, people tend to see patterns when there is none. Sometimes, we also twist that logic just so it fits our expectations.
In gambling, if you believe that a prior streak of events has any effect on the current outcome, then you're the exact type of person casinos would love.
It stands to reason that if a ball lands on a red space in roulette 8 times, then the logical conclusion is that the ball now has a higher probability of landing on a black space, right? Well – no, not really.
This exact thinking is what is called the Gambler's Fallacy. What is it, and how does it affect lottery players? Let's talk.
What is the Gambler's Fallacy?
The Gambler's Fallacy refers to the belief that, if a streak of events occurs, then the next event will most likely break that streak. This belief is also known as the Monte Carlo Fallacy or the Roulette Fallacy.
Let's take roulette as an example. When “reds” come up in succession, players tend to bet on “black” more. It seems logical: people think that they're outsmarting sneaky casinos by betting on “black” and breaking the streak.
In reality, it's the opposite of logical. The odds of you hitting “red” or “black” are the same as they ever were. They're not affected by previous outcomes.
Just because you had a lucky streak, doesn't mean that the chances of you continuing that streak suddenly change. Don't believe me? Let's take a look at a fair coin toss .
The Fair Coin Toss
In a fair coin toss, the probability of you getting heads in one flip is 1 in 2, or 50% (because you only have two outcomes – heads or tails).
Meanwhile, you have a lower probability of flipping the coin twice and getting heads on both attempts.
We can calculate this by multiplying the probability of each coin toss – that is, 50% x 50%. This equates to 25%, or 1 in 4.
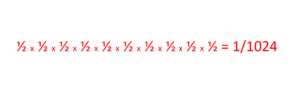
Now, if you calculate your chances of getting heads ten times in a row, that would equate to 1/1024. It's still possible, but highly unlikely.
This is where the Gambler's Fallacy kicks in. Because of how unlikely it is to get ten heads in a row, players go for the outcome that is the most likely one. In this case, you are more likely to choose tails. This behavior is fueled by cognitive bias.
Fallacies are Examples of Cognitive Bias
Cognitive bias refers to the assumptions we tend to make. When it comes to gambling, we tend to assume that some events are more likely than others, even if we don't have concrete evidence to support this.
Going back to the coin toss example: When people see that they have a 1 in 1024 shot of getting ten heads in row, they immediately switch gears.
Because of the Gambler's Fallacy and our inherent cognitive bias, we do this without assessing the situation. In the coin toss example, most of us look at the equation all wrong.
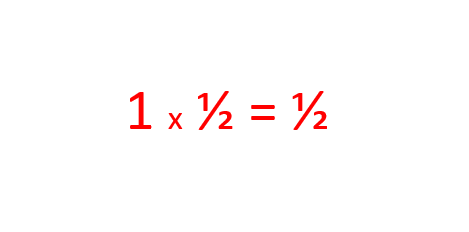
See, it's true that the probability of getting ten heads in a row is 1 in 1024. But that doesn't mean that each toss influences the probability of the next.
Look at it this way: The chances of you getting two heads in a row are 1 in 4, right?
But when you get heads the first time, that means, for that particular toss, the probability becomes 100%. It already happened so it's not an unknown factor anymore.
That leaves your next toss with a 50%, or 1 in 2, probability.
The Hot Hand Fallacy
There's another fallacy that you should keep in mind: the Hot Hand Fallacy. This refers to people's belief that if they get a lucky streak, then their lucky streak will continue.
It's easy to fall into this line of thinking – you feel invincible, so you think there's no way you're losing. However, you must always remember that each turn stands on its own. If you win 3 times, that has no bearing on your 4th try. You may or may not win.
How Cognitive Bias Affects Your Lottery Chances
Lotteries are rife with players that are affected by these fallacies. A lot of players tend to cherry pick from numbers that have been drawn consecutively, for starters.
While that certainly is not a bad thing, it doesn't guarantee you will match the winning numbers, either. If anything, doing so can limit your chances of winning. Plus, other players are also bound to get the same idea as you.
For example, the September 2009 drawing for the Bulgarian 6/42 lottery yielded six numbers that were drawn in two consecutive weeks. No one won the first draw, but 18 players had the same idea and picked the same winning numbers for the second draw.
They all won, but had to share the prize. Needless to say, each player came home with a much smaller prize than they had hoped for.
Finally, falling into the traps of these fallacies can also cause you to spend/lose more money.
For starters, some players keep playing the same numbers over and over, hoping to win one day. Some players, meanwhile, tend to buy more tickets simply because they think they can predict the outcome based on the previous winning numbers.
The problem is there is no “pattern” to observe in lotteries. All of it is random, so it's impossible (and rather foolish) to predict what numbers are going to be drawn. Unless you're psychic, the lottery is and always will remain a game of chance – nothing more, nothing less.


